Answers to the Pyramid Fraction Exercise

 The problem is to build a Pyramid using small blocks of tan and white starting with a base of 9 x 9 blocks and building up from there.  There must be a ratio of 1 out of 5 blocks in the Pyramid being tan, and the remaining white.

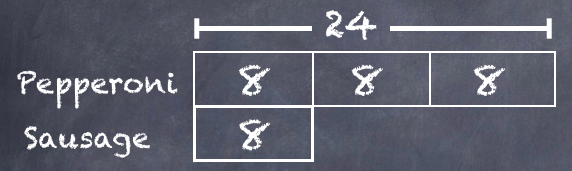
The problem also states that the blocks will be manufactured using a batch method.  The "Mixed" batch will make 3 tan blocks and 1 white one.

The other batch will make all white blocks.

The question is then how many "Mixed" batches will be required to make enough Tan blocks?...and correspondingly, how many regular batches will be required to make up the remaining white blocks?

The first step is to calculate the total number of blocks required.  The problem almost gave us the answer:

Adding up each layer, the total is 140 blocks.

The second step is to calculate the total number of tan blocks required.  Since the ratio is 1 tan block for every 5 blocks, the total number of tan blocks required is 28.

Now the hard part...how many mixed batches are required?

The are 3 tan blocks per one mixed batch.  Divide this into the total number of tan blocks required to find the number of mixed batches. (we are trying to find the number of "groups of three" fit inside the number 28).

Since there are a little over 9 mixed batches required, we best make 10 batches...and eat the left over blocks...unless you painted them, then never mind.

Now to find the white ones:  We know there are 140 total blocks, and 28 of those are tan.  hence, the total number of white blocks are 

140 - 28 = 112 white blocks

We previously made 10 "mixed" batches which each had 1 white block.  No fraction division required here, we know we have 10 white ones from the mixed batches.

112 - 10 = 102 white blocks remaining

We repeat the division process with the regular batches using the ratio of 4 white blocks per batch:

We need 25 1/2 regular batches, so we might as well make 26 and find a use for the left overs.

Just a Fraction of a Fraction

Fractions can be tough, particularly when you are trying to add, subtract, multiply, or heaven forbid divide them!  …and speaking of divide…why in the world would you want to divide two different fractions?  We’ll look at a few examples below.

The key to remember with fraction division is that the fraction below the line (that is, the denominator) is inverted then multiplied against the other fraction which is above the line.  For example:

Fractions Q1:  

Dad is barbecuing ribs again, and he sends you to the store for his favorite BBQ sauce:  "Bubba’s Down Home That’s What I’m Talking About BBQ Sauce”.  He already pre-paid for the ribs, but you need to buy enough sauce for the quantity of ribs he ordered.  He says is uses 3/4 of a cup of BBQ sauce for every 1/2 pound of ribs.  When you get to the store, you find out he ordered 5 1/2 pounds of ribs.  

How many cups of sauce do you need to buy?  What is the final ratio of cups per pound?

A:  The question is for a quantity of sauce, so set up the fraction with the cups of sauce on top to get cups/pound:  

We now know there are 1 1/2 cup for every pound of ribs.  Now find how much sauce we need for 5 1/2 pounds of ribs:

We need 8 and 1/4 cups of sauce.

Fractions Q2:  For every 1/2 cup of "Bubba’s Down Home That’s What I’m Talking About BBQ Sauce” you buy, Dad also adds 1/4 tablespoon of chili powder.    He has about 4 table spoons of chili powder at home, and asks you to pick up the remaining amount at the store.  How many table spoons of chili powder do you need to buy?

A:  The question is asking for an amount of chili powder, so set up the fraction with Chili powder on top:

Total amount of chili powder required = 

16 1/2 cups of sauce x 1/2 tbls of chili / cup of sauce = 8 1/4 tbls of chile

Amount of chili powder to buy = 8 1/4 tbls (total required)  - 4 tbls (at home) 

= 4 1/4 tbls of chili powder to buy


Fractions Q3:  Pyramid Construction

The class is building a pyramid using small blocks (such as sugar cubes) to resemble the stones.  The Pyramid will start with a base of 9 x 9 blocks, then 8 x 8, 7 x 7, and so on.

Levels of the Pyramid:

The Pharaoh for which this Pyramid is being constructed was well respected, so we will honor him with a Pyramid having  some color

consisting of a few tan blocks mixed in with the white ones (the class can use natural or brown sugar cubes, or paint, etc. for the tan colored blocks).

The ratios are:

• 1 Tan block in every 5 blocks
• 4 white blocks in every 5 blocks

(in other words, out of every group of 5 blocks, 1 of those will be tan, and the remaining four will be white)

We're going to emulate the ancient method of manufacturing blocks (actually used to make old adobe missions) by using a batch method - 4 blocks per batch.  One batch of blocks (the "mixed" batch) will make 3 tan blocks and 1 white block .  The other batch will make all 4 white blocks.

Hence, there is a ratio of 3 Tan blocks per 1 Mixed Batch.

One half of the class will be responsible for the "mixed" batches.  The other half of the class will be responsible for the regular all-white batches.

How many "mixed" batches will be required to make enough tan blocks to meet the required quantity? 

How many regular batches of white blocks will be required to make the remaining amount of blocks for the Pyramid?

Note:  if you come up with an answer which is not an integer, but instead includes a fraction, then just round up to the next integer.

Find Your Fast-Food Fraction!

So many on-line quizzes available today:  What color of the Rainbow are your like; Which Disney Princess are you like; which iconic movie character are you born to play; which Storm Trooper do you resemble?...the list is endless.

So why not one more?   What is your Fast-Food Fraction?  Find your Fraction based on your favorite fast-food.  Follow the map below to find your fraction assignment, then adjust the fraction by using the Fast-Food Fraction Adjustment Table below the Map.

Important Safety Tip:  Some fraction addition or subtraction may be required.

If you cannot figure out your fraction, perhaps you should:

a.  Stick with integers, or 

b.  Study some of the fraction-related posts further on in this blog site.

Good Luck!

Fast-Food Fraction Map

11. Percentages: 50% More Fun!

You can have 50% of the fun…or 50% more fun…or half as much fun…or even half-again as much fun. Are these all the same?  They all use 50% or the word "half", but the slight addition of a few different english words changes the meaning drastically.   

Half or 50% of the Fun is giving you 50% of the total - hence you are enjoying this post only half as much as you could.

However, 50% more Fun or Half again as much Fun are providing words that imply adding more to the total.  In this case, you are giggling all of what I would expect, plus another 50% to make a total of 150% total giggling.

In a previous post on Rates, I wrote that Percentages always add up to 100%.  Well, I must have been smokin’ something.  Of course you can have a Percentage more than 100%.  By simply reading this post, you are having 50% more, or 150% of the Fun compared to other people who are having only 100% of the fun reading some other lame math post.   

Let’s try another example of percentages greater than 100%.  You want to borrow $100 from me..and you agree to pay me back the $100 by the end of the week plus an additional 20% interest (I have a friend Guido who will make sure you do).  I stand to realize 120% gain on my investment:  100% being the total amount I loaned to you paid back plus an extra interest of 20%.   

When word problems use standard percentages like 30% or 25%, it is assumed that they are using 100% as the total.  It is the whole pie.  100%.  You cannot have more than the whole pie...unless of course they add more pie to the problem.  My $100 I loaned to you was the 100%.  When I asked for an additional 20% interest, I just added more pie.

Often, word problems will tell us the total amount (the 100%) and ask you to solve for a missing percentage.  For example, there are 30 children in the classroom (Whoa - see what happened there??  It just defined the total...the 100%), and there are 20% boys.  What is the percentage of girls in the class?  In this case, they must add up to 100%.  Obviously the percentage of Girls in the class is 80% (100% - 20% = 80%).  

One last fun point on Percentages.  Common Core may require the ability to describe percentages in a variety of forms.  The tests may provide one form, and ask to define the other forms: 

Percent Fraction:  It is the percent, but instead of showing the “%” sign, we show the number divided by 100.

Percent:  It is the same number as used in the Percent Fraction above except followed by the “%” sign instead of dividing by 100.  Think of the “%” sign meaning “divided by zero”.

Fraction:  One number over another number usually defined in its lowest possible form (i.e. write 1/4 instead of 2/8).  This fraction would be the same as Percent if you were to divide the top number by the bottom number.  For example:  1/4 is the same as 0.25 if you divided the number 1 by the number 4.  

Decimal:  The Decimal number is the same as the Percent Fraction number if you divided the top number by 100.  For example, 0.25 is the same as 25/100.

Below is a table showing some examples of the various forms.

Boy-oh-boy could we have more fun with Percentages?  I think not!  Maybe I should have labeled this Post as 75% more fun.

10. Answers to Tape Diagrams

Answer to Tape Q1:

The ratio of pepperoni to sausage is 3 to 1.  We used up 24 slices of pepperoni.  How many pieces of sausage did we use?

We can see from the problem that the ratio is 3:1.  So we need three boxes and one box.  We also know the total Pepperoni is 24.  So set up the Tape diagram with what we know: 

Next:  figure the magic number (remember:  all of the numbers inside the boxes must be the same). What goes into 24 equally three times?…why the number 8 of course.  Write the number 8 in all of the boxes.   

Now calculate the quantity of sausage used (Hmmm, let’s see…. 1 times 8 = 8!!!).

Answer to Tape Q2:   It’s Pizza Day at the cafeteria Can’t get enough of that Pizza).  There are two cafeteria lines - Sixth graders in one line and Fifth graders in the other.  There are two Sixth graders for every three Fifth graders.  You count 40 Sixth graders in your line.  How any Fifth graders are in line?

Set up the Diagram with what we know:  

•  A ratio of 2:3 (sixth graders to fifth graders).  Hence show two boxes and three boxes.  Label the three-box row "fifth graders" and the two-box row "sixth graders”.
• We also know the number 40 for the total sixth graders - so 40 on the sixth grade line.  Your diagram should now look like this: 

Next:  Find the magic number:  Two sixth graders boxes add up to 40.  The magic number must be 20 (40 divided by 2).   Now write 20 in all of the boxes.

Add up the number of “20s"in the fifth grade boxes and write the total in the fifth grade line on top (which should be 60).   Voila. 

Answer to Tape Q3:  You have major math homework tonight - 30 math problems…YIKES!.  You are also starving for those homemade Chocolate Chip cookies.  Mom says you can have two cookies for every 6 math problems you work out correctly.  You finish all of the math homework correct.  How many cookies do you get?

What do we know?

• The Ratio is 2 cookies to 6 Math, or 2:6.  (hence two boxes and six boxes)
• The bonus number is the total Math problems at 30.

Set up the diagram: 

Now solve for the magic number.  Six equal boxes adding up to 30.  (30 divided by 6 = 5).  Write “5" in all of the boxes.

  The quantity of cookies is 10.

9. Get it on Tape (Diagrams)

Tape Diagrams are yet another method for graphically or visually solving ratio-type word problems. It is slightly different than Double Lines or Equivalence Tables.

Tape-type word problems typically include a ratio of two things (two of These to three of Those) plus a bonus of one other number which is typically the total of one of the items.  For example:  The ratio of Apples to Oranges is 4:3.  We have 24 Apples….how many Oranges do we have?  See?  What did I tell you?  This problem gave us the ratio of the two items plus a bonus number of the total of one of the items.

When you set up a Tape Diagram for this type of problem, you simply show the ratio in the form of a bunch of boxes (it’s supposed to resemble some sort of  piece of tape).  

The drawing at right shows two Tape Diagrams, one for a ratio of 3:2 and the other a ratio of 4:3.   

To diagram the 4:3 ratio of apples-to-oranges problem above, we would draw four boxes in a row to resemble the apples, and then three boxes in a row for the oranges. 

Important Safety Tip:  Always make the boxes the same size, and always line them up on the left.

Next, label the rows of boxes.  We can also add the bonus number we know, which from the problem is 24 apples.  Show that number across the top of the Apples. 

The problem is asking for the total number of Oranges…which is the bottom number.

Now here’s the tricky part:  We want to place a number in all of the boxes, and that “magic" number will be the same number in all boxes.  There is only one number which fits (that’s why it is a magic number).  To figure out that one magic number, we look at the row of boxes for the item which we know the total number - in this case it is the total of 24 apples.  Since we have four boxes, and the number is always the same number in all boxes, we divide (in our head) the total of 24 by the number of boxes in that row (4).  

Another way to think of this is:  you have a total of 24 apples in a pile.  You need to put an equal number of apples in each of the four boxes.  You start by putting  one apple in each box and keep repeating until all of the apples are gone.  You would end up with 6 apples in each box.  Hence,  24 divided by four is six.  So the magic number is 6.

Now here’s the fun part: Since the magic number is 6, put a "6" in each of the Oranges boxes.  There are 3 boxes of 6. 

So, again, we do in our head “3 times 6 equals 18” , and write 18 in the bottom total for Oranges.

Another important safety tip:  These types of Tape Diagram problems always lend themselves to using numbers which are easily divisible by other numbers.  We usually do not see a ratio of 4 1/2 to 3 (where it’s tough to draw four and half boxes on top), or a ratio of 4:3 with a total of 23 (where 4 doesn’t divide into 23 very easily).  

Now try a few problems (answers to follow in another follow-on post):

Tape Q1:  We’re making pizza!  The ratio of pepperoni to sausage is 3 to 1.  We used up 24 slices of pepperoni.  How many pieces of sausage did we use?

Tape Q2:   It’s Pizza Day at the cafeteria (can’t get enough of that Pizza).  There are two cafeteria lines - Sixth graders in one line and Fifth graders in the other.  There are two Sixth graders for every three Fifth graders.  You count 40 Sixth graders in your line.  How any Fifth graders are in line?

Tape Q3:  You have major math homework tonight - 30 math problems…YIKES!.  You are also starving for those homemade Chocolate Chip cookies.  Mom says you can have two cookies for every 6 math problems you work out correctly.  You finish all of the math homework correct.  How many cookies do you get?

Good Luck!

8. Answers to Double Lines

Answer to Double Line Problem #1:

There are 20 girls in the class, and the ratio of Girls to Boys is 4:3.  How many Boys?
Draw the two parallel lines & label one "Girls"and other "Boys".

We are solving for Boys, so start with Girls.  Since there are "4" Girls per whatever and a total of 20 Girls, draw a series of vertical lines and label each one with increments of 4 (on the Girls line) until you get to 20.

Next: Since for every 4 Girls there are 3 Boys, we are going to use increments of 3 on the Boys line. Under the Girls "4", write a "3" on the Boys line, then a "6" under the Girls "8", then "9", "12", and finally "15" under the Girls "20".  Your Line Diagram should look like this:

There answer is 15.


Answer to Double Line Problem #2:
For every handful of popcorn I grab to eat, I drop 2 kernels to the floor.  Every handful of popcorn has eight kernels in it. The bowl of popcorn gave me 9 handfuls.  How many kernels landed on the floor?  

This one is a little tough so bear with me.  Here's what we know:

• 2 kernels dropped per handful.
• 8 kernels per handful
• 9 handfuls total.

We need to find:  Quantity of kernels on the floor.

The "handful" makes it a little confusing, however, we are solving for the number of kernels on the floor, so we need to break everything down into kernels and forget the handful nonsense.

8 kernels per handful and 9 handfuls total means there are 72 kernels total (8 x 9 = 72).

The ratio is 2 kernels to 8 kernels (per handful), or 2:8.

Draw up the double lines and use the labels "Dropped" and "Handful".  Start labeling the "Handful" line with increments of 8 until you get to the total of 72.  I grabbed 9 handfuls of 8, so there are 9 vertical lines (not including the zero line).

On the "Dropped" line, label the vertical lines with increments of 2 starting from zero.

The answer is 18 kernels on the floor for the dog to eat.

7. Seeing Double (Lines)

Another graphical method for deciphering and solving word problems is the use of Double Number Lines.  This technique uses the same approach which we used earlier with Equivalence Tables...only Double Number Lines go horizontally, and Tables go vertically.  (It may be helpful to review the Post on Equivalence Tables if you have not already done so).

If you remember the example problem from the post on Tables:  Three boys can eat two pizzas.  How many pizzas will be required to feed 15 boys?  Let us apply Double Number Lines to this problem.


Draw two horizontal parallel lines, and mark one "Pizzas" and the other "Boys".  Since the problem is asking to solve for Pizzas, begin with the Boys line and starting from zero, place marks on the line in increments of 3 (since we know that it will take 3 boys for every 2 pizzas) until you get to 15 Boys.

Now, on the Pizza line, place increments of 2 along the same marks.  Since we know that 3 Boys eat 2 Pizzas, put a 2 under the 3, and then add increments of 2 to each subsequent mark.

When you get to 15 Boys, we'll have the answer of 10 Pizzas.

As you see, the approach is nearly identical to how we set up Equivalence Tables.

Unit Rates
A side benefit of Double Number Lines is that we can use them to graphically determine Unit Rates.  We didn't discuss Unit Rates in earlier Posts...so here we go:

How many miles per gallon does your car get?  Don't answer, or stop and go out to check your car's specifications...I really don't care what your mpg is.  The point is that mpg is a unit rate.  It defines how many miles you can drive in one gallon (e.g. miles per gallon).  Miles per hour is another Unit Rate...it defines how many miles you travel in 1 hour.  Saying you are driving 80 miles in an hour and a half is not very helpful.

There will be word problems in Common Core asking to determine a unit rate.

Going back to our Boys/Pizza problem, we can use the Double Number Lines to determine the unit rate of Boys/Pizza.  Since we want to know how many Boys per one Pizza, find the number 1 on the Pizza line & label it.  Since we started with 2 Pizzas on the line, 1 Pizza is halfway between the 2 and Zero.

Now, make a mark on the Boys line directly above the 1 Pizza mark and label it.  Since we know that the 1 Pizza mark was halfway between the 2 mark and zero, the new Boys mark must also be halfway between the 3 mark and zero.  Hence, the number of Boys per Pizza is half of 3 which is 1 1/2 Boys per Pizza (or 1.5 Boys/pizza).

We could have found the opposite - the number of Pizzas/Boy - but the process is a little more complicated.  Because we need to find the quantity of Pizzas per one boy, find a mark for 1 boy on the Boys line, which is 1/3 distance between 0 and 3.

The corresponding Pizza mark would then be 1/3 the distance between 0 and 2...which is, um, let's see, hmm...carry the one....2/3 Pizzas.  Hence, the unit rate is now 2/3 pizzas/boy (or 0.667 Pizzas/Boy).

Now a couple of test questions:

Line Q1: There are 20 girls in the class.  The ratio of girls to boys is 4:3.  Use Double Number Lines to determine the number of boys in the class.

Line Q2:   For every handful of popcorn I grab to eat, I drop 2 kernels to the floor.  Every handful of popcorn has eight kernels in it. The bowl of popcorn gave me 9 handfuls.  How many kernels landed on the floor?

6. A Few Words About Nothin (i.e. Zero)

In a previous post, we dabbled a bit in ratios.  However, I failed to mention at that time that the denominator, the number below the line, the second number of a ratio, shan't be a Zero. Many word problems dealing with ratios may provide a word problem having a ratio of a/b and then quickly add where b is not equal to zero.

The reason is this:  you cannot divide a number by Zero.  It's not allowed, it's against the law of mathematics, I'm sure it violates some federal law and maybe even the Constitution, and besides, it just ain't fittin.  Only terrorists divide by zero.

If you find yourself faced with a ratio or fraction type problem where the denominator is zero...STOP!   Put down your pencil.  And call the authorities immediately.

5. Equivalence Tables & Coordinate Graphs

Well, back in MY day, we converted word problems directly to equations...and we liked it.  (well, maybe we didn't like it...but we did it).  Now, the Common Core wants us to solve word problems using a variety of visual methods such as Equivalence Tables and Coordinate Graphs.

This post will explore the concepts of each of these alternative problem solving methods.  

Equivalence Tables: 

Equivalence tables are one option for solving ratio problems.  The way this works is you set up two columns (which actually represents the ratio).  In the left column, put one of the ratio numbers, and place the other number in the right column.  

For example:  Three boys can eat 2 pizzas.  There are 15 boys.  How many pizzas will be required?

Set up two columns with five or six rows.  Make the Boys column be the one on the left (although which side doesn't really matter) and the Pizza column on the right.

In the first row, place the number of boys in the left column (i.e. "3"), and the number of pizzas in the right (“2”).  This is the basic ratio 3:2.

We need to find the number of pizzas to feed 15 boys.  So what we are going to do is walk down the column adding “3" to each number in the left column, and “2" to the numbers in the right column.  The numbers we use [3 and 2] are whatever the numbers are in the very first row. 

We continue to add the number 3 to the left column and 2 to the right column.  When the number in the left column finally reaches the target (i.e. 15), stop.  The answer to the quantity of Pizzas required will be in the right column (i.e. 10).

Good thing we don't have 150 boys...we'd be here all night.

How this works (if you care to know):  In the left Boys column where we keep adding 3’s, the second row is actually two 3’s, the third row is three 3’s, the fourth row is four 3’s, and the fifth is five 3’s.  The right Pizza column: the second row is two 2’s, then three 2’s, then four 2’s, and finally five 2’s.  If we kept on going, then the next row would be six 3’s and six 2’s, hence 18 boys would require 12 pizzas. Each row represents the same, identical ratio:  3:2, 6:4, 9:6, 12:8, 15:10 ...they are all 3:2.

Woe be us if the total number of boys is not easily divisible by 3.  If the total number of boys were, say, 16, then this method breaks down.


Coordinate Graphs

Well, now that we have mastered THAT, let's move right into applying the same problem in a Coordinate Graph.  Applying the table to a Coordinate Graph is very straight forward.  Using the table  from the previous problem, assign one column as the "X" axis, and the other column of numbers as the "Y" axis.  Now draw a graph with X axis going to the right, and the Y axis going up assigning numbers on each axis.  

Now plot each pair from the table on to the graph:

First row pair 3,2 : go to 3 on the X axis and then go up 2 on the Y axis & place a point.

Second row pair 6,4:  Find 6 on the X axis and go up to 4 on the Y axis & place another point.

Repeat for all points on the table and it should like the one below.

You know you've done this correctly when all of the points line up in a perfectly straight line.  This means that each pair of numbers represent the same ratio.  If any point does not lie on that line...or the line curves for some strange reason, you best double check the table.

You can also use the graph to extrapolate for other numbers.  For example, if there were 17 boys, then you go to 17 on the X axis, and go straight up to where the line of points would intersect with 17 from the X axis.  From this point, make a straight line over to the Y axis.  Where that line intersects the Y axis is the # of Pizzas required.   

From the graph, it looks like you would need 11 1/2 pizzas.  Of course, you would order 12 whole pizzas, and take the extra 1/2 pizza home for dinner.  Then the School Principle finds out you absconded with the extra pizza for your own personal gain without reimbursing the school and you end up in the Principle's office the next day trying to explain yourself.  I don't have a graph for that...you're on your own.

What would a ratio graph look like if you made a mistake while setting up the table?  Let's have a look.



Zach set up a table of Equivalences...but he made a mistake on one of the entries.  Plot the number pairs on a graph and circle the mistake.  


As you can tell from the chart below, the fourth number on the graph is not really in line with the first three.  You can also tell by following the path along the first three points.  

 Starting at 0,0, you go over to 4 and up 3 to get to the first point...then over another 4, and up another 3 to get point #2.  Go over 4 and up 3 to get point #3.  As you go over 4 and up 3 again, you realize that the fourth point is not where it should be.  It is out of place.  Once this happens, then the other points follow along and the whole thing is just a Dogs Dinner.








If we go back to the table, we see that the fourth number in the X column is a 15 which should have been 16 (12 + 4 = 16).  


Boy, that Zach....what a card.

Here are a few problems to try.  The answers will follow on another post...some day.

Table Q1:  The ratio of boys to girls in the classroom is 3:5.  You count 18 boys.  How many girls are there?  Use an equivalence table.

Table Q2:  Plot the following table on a Graph.